Lab #7: Dijkstra’s Shortest-Path Tree

Description

This activity must be developed in the pre-assigned teams of two.

In a file called dijkstra.py, write a Python function called dijkstra_spt that takes as input an initial vertex and a connected undirected weighted graph. The function uses Dijkstra’s algorithm to find the shortest-path between the initial vertex and all the other graph’s vertices. The function returns a tuple with two items:

1. A costs dictionary where each key \(k\) is a vertex and its associated value is the cost of going from the initial vertex to the vertex \(k\).
2. The resulting spanning tree with the shortest-path from the initial vertex to every other one.

For example, given the following weighted graph:

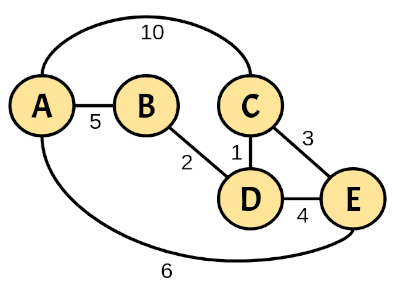
The resulting costs dictionary with initial vertex A is:

Vertex	Cost
A	0
B	5
C	8
D	7
E	6

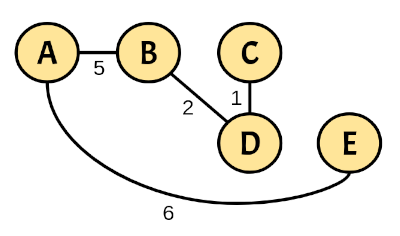
The graph that represents the shortest-path spanning tree is:

This is how the dijkstra_spt function should be called:

dijkstra_spt('A', {'A': {('B', 5), ('C', 10), ('E', 6)},
                   'B': {('A', 5), ('D', 2)},
                   'C': {('A', 10), ('D', 1), ('E', 3)},
                   'D': {('B', 2), ('C', 1), ('E', 4)},
                   'E': {('A', 6), ('C', 3), ('D', 4)},
                  })

Note that strings are used to represent the vertices, while the graph is represented as a dictionary where each key is a string and its associated value is a set of tuples (the vertex’s neighbours) containing a string and a number (the respective edge’s weight).

The previous function call returns the following result:

({'A': 0, 'B': 5, 'C': 8, 'D': 7, 'E': 6},
 {'A': {('B', 5), ('E', 6)},
  'B': {('A', 5), ('D', 2)},
  'C': {('D', 1)},
  'D': {('B', 2), ('C', 1)},
  'E': {('A', 6)}})

Use the following code as a starting point:

# File: dijkstra.py

WeightedGraph = dict[str, set[tuple[str, float]]]


def dijkstra_spt(
        initial: str,
        graph: WeightedGraph) -> tuple[dict[str, float], WeightedGraph]:
    # The function's code goes here
    ...

NOTE: When choosing the shortest distance from the set of unvisited vertices, if there happens to be a tie with two or more vertices then choose the vertex with the name that comes first in lexicographical (alphabetical) order. If you do not follow this indication your code might have some issues with the unit tests (it might fail even if a technically correct solution is produced).

Test your code using the tests in the file test_dijkstra_spt.py. Finally, make sure no type or PEP 8 style errors are produced by using the mypy and pycodestyle linters. You can run them at the terminal like this:

mypy cryptarithmetic_puzzle.py

pycodestyle cryptarithmetic_puzzle.py

Deliverables

Place in a comment at the top of the dijkstra.py source file the authors’ personal information (student ID and name), for example:

#----------------------------------------------------------
# Lab #7: Dijkstra’s Shortest-Path Tree
#
# Date: 17-Nov-2023
# Authors:
#           A01770771 Kamala Khan
#           A01777771 Carol Danvers
#----------------------------------------------------------

Only one team member needs to upload the file.

Due date is Friday, November 17.