Lab #4: A* Search Algorithm

Description

This activity must be developed in the pre-assigned teams of two.

Using the updated generic_search module developed in chapter 2 of [KOPEC], write a Python script called fifteen_puzzle.py that solves the 15 puzzle using the A* search algorithm as described in section 2.2.5. It is highly recommended that you reread at least this particular section of the book to make sure you have an adequate understanding of the algorithm being used.

The 15 Puzzle

As defined in Wikipedia:

The 15 puzzle is a sliding puzzle having 15 square tiles numbered 1 to 15 in a frame that is 4 tiles high and 4 tiles wide, leaving one unoccupied tile position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to place the tiles in numerical order.

For example:

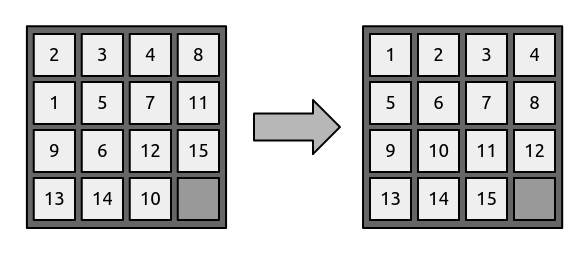
Here we start with the frame configuration at the left. We want to obtain the final configuration at the right, where all numbers are in order. What are the steps required to go from start to finish? The solution requires 16 steps:

1. Move 15 down
2. Move 12 right
3. Move 10 up
4. Move 15 left
5. Move 12 down
6. Move 11 down
7. Move 8 down
8. Move 4 right
9. Move 3 right
10. Move 2 right
11. Move 1 up
12. Move 5 left
13. Move 6 up
14. Move 10 left
15. Move 11 left
16. Move 12 up

Implementation Details

In your fifteen_puzzle.py script, write a function called solve_puzzle that takes as input the initial frame configuration. Use the following code as a starting point:

# File: fifteen_puzzle.py

from typing import Optional
from generic_search import astar, Node, node_to_path

Frame = tuple[tuple[int, ...], ...]


def solve_puzzle(frame: Frame) -> None:
    result: Optional[Node[Frame]] = astar(
        frame, goal_test, successors, heuristic)
    # The rest of the function's code goes here
    ...


# The rest of the module's code goes here
...

A frame configuration is of type Frame which is a tuple of tuples of ints. The astar function takes four arguments, the last three are: goal_test, successors, and heuristic. These are functions that you will need to implement and they are discussed below.

Once the astar function terminates it returns a Node[Frame] if a solution was found, or None otherwise. If you do get a valid solution, use the node_to_path function to get a list with all the configuration frames in the order that solves the puzzle. Translate these configuration frames to the corresponding text that explains which tiles to move to produce the exact expected output shown below.

When testing your code, you should be able to call the solve_puzzle function like this (note that the value 0 in a frame configuration represents the unoccupied tile):

solve_puzzle(((2, 3, 4, 8),
              (1, 5, 7, 11),
              (9, 6, 12, 15),
              (13, 14, 10, 0)))

For this example, the program should print to the standard output the following text:

Solution requires 16 steps
Step 1: Move 15 down
Step 2: Move 12 right
Step 3: Move 10 up
Step 4: Move 15 left
Step 5: Move 12 down
Step 6: Move 11 down
Step 7: Move 8 down
Step 8: Move 4 right
Step 9: Move 3 right
Step 10: Move 2 right
Step 11: Move 1 up
Step 12: Move 5 left
Step 13: Move 6 up
Step 14: Move 10 left
Step 15: Move 11 left
Step 16: Move 12 up

As stated before, you will need to provide the implementation of the following three functions in order for the A* algorithm to work correctly:

Function Signature	Description
def goal_test(     frame: Frame ) -> bool:	Returns true if the input frame is equal to the goal configuration, otherwise returns false. Remember that the goal configuration is: ((1, 2, 3, 4),  (5, 6, 7, 8),  (9, 10, 11, 12),  (13, 14, 15, 0))
def successors(     frame: Frame ) -> list[Frame]:	Returns a list with all the possible frame configurations that are one move away from the input frame. So, for example, if frame is: ((2, 3, 4, 8),  (1, 5, 7, 11),  (9, 6, 12, 15),  (13, 14, 10, 0)) the unoccupied space (where the 0 is located) determines that there are two valid moves from this configuration: slide the 15 down or slide the 10 to the right. Thus, this function should return the following list: [((2, 3, 4, 8),   (1, 5, 7, 11),   (9, 6, 12, 0),   (13, 14, 10, 15)),  ((2, 3, 4, 8),   (1, 5, 7, 11),   (9, 6, 12, 15),   (13, 14, 0, 10))] NOTE: In order to pass all the unit tests your implementation should return the list of frame configurations in the following movement order: $$ [\textit{Up}, \textit{Down}, \textit{Left}, \textit{Right}\,] $$
def heuristic(     frame: Frame ) -> float:	A heuristic function ranks alternatives in search algorithms at each branching step based on available information to decide which branch to follow. In this particular case, our heuristic function should return the amount of numbers that are NOT in their final position (including the 0 for the unoccupied space). For example, if frame is: ((2, 3, 4, 8),  (1, 5, 7, 11),  (9, 6, 12, 0),  (13, 14, 10, 15)) the function should return 12.0

Test your code using the tests in the file test_fifteen_puzzle.py. Finally, make sure no type or PEP 8 style errors are produced by using the mypy and pycodestyle linters. You can run them at the terminal like this:

mypy fifteen_puzzle.py

pycodestyle fifteen_puzzle.py

Deliverables

Place in a comment at the top of the fifteen_puzzle.py source file the authors’ personal information (student ID and name), for example:

#----------------------------------------------------------
# Lab #4: A* Search Algorithm
# Solving the 15 puzzle.
#
# Date: 06-Oct-2023
# Authors:
#           A01770771 Kamala Khan
#           A01777771 Carol Danvers
#----------------------------------------------------------

Only one team member needs to upload the file.

Due date is Friday, October 6.