Advanced Algorithms

Overview: Final Exam

Topics

  1. Algorithm analysis review.
    1. Big O notation.
    2. Common runtime functions: \(O(1)\), \(O(\log N)\), \(O(N)\), \(O(N \log N)\), \(O(N^2)\), \(O(N^3)\), \(O(2^N)\), \(O(N!)\). Examples of algorithms for each of these.
  2. Python language specific features.
    1. Type hints.
    2. Bitwise operators: &, |, ^, ~, <<, >>.
    3. Comprehensions: lists, sets, dictionaries, generators.
    4. Generator functions and the yield statement.
    5. Classes, data classes, named tuples.
  3. Combinatorics.
    1. Power set.
    2. Combinations (with and without repetitions).
    3. Permutations (with and without repetitions).
  4. Search algorithms.
    1. Depth-first search (DFS).
    2. Breadth-first search (BFS).
    3. A* search.
    4. Constraint-satisfaction problems (CSP).
  5. Priority queues.
    1. Min heaps and max heaps.
    2. Heap insertion and deletion.
    3. Heapsort.
    4. Python’s heapq module. Functions heappush, heappop, and heapify.
  6. Graphs.
    1. General graph concepts.
    2. Graph traversal algorithms.
    3. Spanning trees.
    4. Minimum spanning tree algorithms (Jarník/Prim, Kruskal).
    5. Dijkstra’s algorithm.
  7. Problem solving design techniques.
    1. Divide and conquer.
    2. Brute-force.
    3. Backtracking.
    4. Greedy algorithms.
    5. Dynamic programming.
  8. Miscellaneous problems.
    1. Adversarial search (minimax algorithm, alpha-beta pruning).
    2. Knapsack problem.
    3. Traveling salesman problem.

Allowed Items During the Exam

NOTE: Once the exam starts you are not allowed to share any items with anyone else.

  1. Pen, pencil, eraser, pencil sharpener.

  2. Simple scientific calculator. You are not allowed to use a cell phone, programmable calculator, tablet, computer, or any other electronic device.

  3. Personal cheat sheet with the following characteristics:


    1. Must be one of these:

      • \(5 \times 8\) inches index card (\(12.7 \times 20.32\) cm).

      • Half letter size sheet of paper (\(13.97 \times 21.59\) cm).

    2. Must be handwritten. Computer-made cards/sheets are not allowed.

    3. You can write in both sides of the card/sheet.

    4. Must include your student ID and full name on the upper-left corner of both sides of the card/sheet.

    5. There are no restrictions on the specific content written on the card/sheet.


Sample Questions

  1. Name an algorithm that has an \(O(2^N)\) complexity.

  2. Given the set \(S = \{ w, x, y, z \}\), calculate the power set of \(S\).

  3. How would you explain the A* search algorithm to a smart ten-year-old child?

  4. You have the following Python code: 

    Vector = list[int]
Matrix = list[Vector]

def e(m: Matrix) -> Matrix:
    def f(i: int) -> Vector:
        def g(j: int) -> int:
            return m[j][i]
        return [g(j) for j in range(n)]
    n = len(m)
    return [f(i) for i in range(n)]

    What is the time complexity of function e? Explain your answer.

  5. Assume that the following code completes the program that started with the code from the previous question. What gets printed to the standard output when running the program? 

    if __name__ == '__main__':
    print(e([]))
    print(e([[1]]))
    print(e([[1, 2],
             [3, 4]]))
    print(e([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]]))

  6. What is the output of the following Python program? 

    def h(n: int) -> list[int]:
    return [x for x in range(1, n + 1) if n % x == 0]


if __name__ == '__main__':
    print(h(19))
    print(h(20))

  7. Write in Python or pseudocode a function called heap_children. The function takes as input a list \(a\) containing a binary heap and an index \(i\). It returns a tuple with the values of the left and right children corresponding to the element contained in \(a[i]\). The tuple should contain None in place of the value of a non existing child. The function’s signature is as follows: 

    def heap_children(
    a: list[int],
    i: int
) -> tuple[Optional[int], Optional[int]]:

    Usage examples: 

    >>> heap: list[int] = [1, 3, 6, 5, 9, 8]
>>> heap_children(heap, 1)
(5, 9)
>>> heap_children(heap, 2)
(8, None)

  8. What is the time complexity of a brute-force algorithm for solving the Traveling Salesman Problem (TSP)?

  9. You have the following weighted undirected graph:

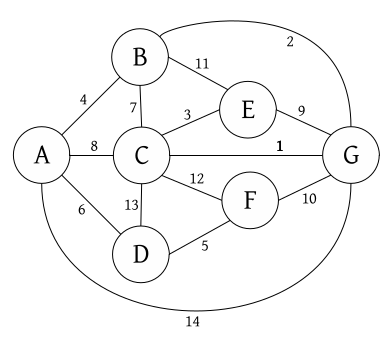
    1. Traverse the graph in DFS (Depth-First Search) order, starting in vertex A. Immediately neighbouring vertices should be processed in alphabetical order.
    2. Traverse the graph in BFS (Breadth-First Search) order, starting in vertex B. Immediately neighbouring vertices should be processed in alphabetical order.
    3. Using Kruskal’s or Prim’s algorithm find the minimum spanning tree (MST). Draw the resulting tree and indicate its total cost.
    4. Apply Dijkstra’s algorithm to find the shortest-path between the vertex C and all the other graph’s vertices. Write the corresponding shortest-path table and draw the resulting graph.

  10. Suppose you’re going camping. You have a knapsack that will hold 6 lb, and you can take the following items. Each has a value, and the higher the value, the more important the item is:

    • Water, 3 lb, 10
    • Book, 1 lb, 3
    • Food, 2 lb, 9
    • Jacket, 2 lb, 5
    • Camera, 1 lb, 6

    Use dynamic programming to build the corresponding table in order to find what’s the optimal set of items to take on your camping trip.