Overview: Midterm Exam

Topics

1. Algorithm Basics. [STEPHENS] chapter 1.
   1. Basic concepts (algorithms, data structures, pseudocode).
   2. Big O notation.
   3. Common runtime functions: \(O(1)\), \(O(\log N)\), \(O(N)\), \(O(N \log N)\), \(O(N^2)\), \(O(N^3)\), \(O(2^N)\), \(O(N!)\). Examples of algorithms for each of these.
2. Memory Management in C++
   1. Correct usage of dynamic memory operators: new and delete for simple objects and arrays.
   2. Implementation of class destructors.
   3. Diagnosing and correcting memory errors (segmentation faults and memory leaks) using Valgrind.
3. Linked Lists. [STEPHENS] chapter 3.
   1. Linear and circular linked lists.
   2. Singly and doubly linked lists.
   3. Node insertion and deletion, sequential traversal.
   4. Lists with sentinel node.
   5. Advantages and disadvantages over arrays.
4. Stacks and Queues. [STEPHENS] chapter 5.
   1. LIFO and FIFO methods.
   2. Inserting and removing elements.
   3. Implementions using linked lists, arrays, and circular arrays.
   4. Evaluation of expressions in postfix notation.
   5. Common examples.
5. C++ Standard Containers, Part I (simple usage and basic operations).
   1. std::list
   2. std::forward_list
   3. std::vector
   4. std::array
   5. std::stack
   6. std::queue
6. Sorting. [STEPHENS] chapter 6.
   1. \(O(N^2)\) algorithms (insertiosort, selectionsort, bubblesort).
   2. \(O(N \log N)\) algorithms (heapsort, quicksort, mergesort).
   3. Sub \(O(N \log N)\) algorithms (countingsort, bucketsort).
   4. C++ std::sort function using a custom comparator.

Allowed Items During the Exam

NOTE: Once the exam starts you are not allowed to share any items with anyone else.

1. Pen, pencil, eraser, pencil sharpener.

2. Simple scientific calculator. You are not allowed to use a cell phone, programmable calculator, tablet, computer, or any other electronic device.

3. Personal cheat sheet with the following characteristics:

   Must be one of these: \(5 \times 8\) inches index card (\(12.7 \times 20.32\) cm). Half letter size sheet of paper (\(13.97 \times 21.59\) cm). Must be handwritten. Computer-made cards/sheets are not allowed. You can write in both sides of the card/sheet. Must include your student ID and full name on the upper-left corner of both sides of the card/sheet. There are no restrictions on the specific content written on the card/sheet.

Sample Questions

1. Name an algorithm that has an \(O(\log N)\) complexity.

2. You have three algorithms: A, B, and C. Algorithm A has a performance of \(O(N!)\). Algorithm B has a performance of \(O(N^3)\). Algorithm C has a performance of \(O(2^N)\). Which algorithm has the best performance? Which one has the worst?

3. You have the following C++ code:

   #include <iostream>
   #include <vector>
   
   int f(int x)
   {
       int r = 0;
       while (x) {
           x /= 2;
           ++r;
       }
       return r;
   }
   
   void g(int n, std::vector<int>& v)
   {
       for (int i = 0; i < n; ++i) {
           v.push_back(f(i));
       }
   }
   

   What is the time complexity of function g? Explain your answer.

4. Assume that the following code completes the program that started with the code from the previous question. What gets printed to the standard output when running the program?

   int main()
   {
       std::vector<int> v;
       g(10, v);
       for (int x : v) {
           std::cout << x << " ";
       }
       std::cout << "\n";
       return 0;
   }
   

5. When trying to find a certain item inside a linked list, which search algorithm should be used and what is its time complexity?

6. Assume you have the following C++ struct declaration:

   struct Node {
       int value;
       Node* next;
   };
   

   Using this structure it is possible to create a singly linked list using dynamic memory. For example:

   

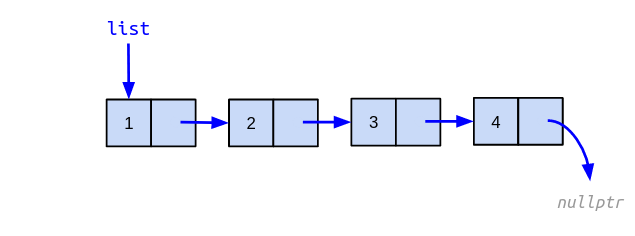
   Write a reverse function that inverts a linked list by changing the links between nodes. No new nodes should be created. The value field of the nodes should not be modified. For the list shown above, the resulting inverted list should be as follows: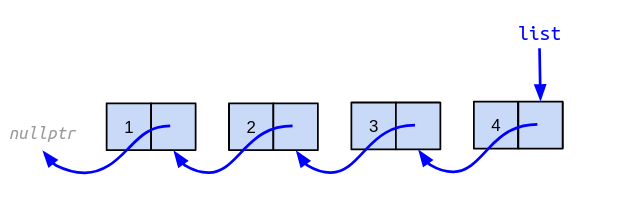

   

   The signature of the reverse function should be:

   void reverse(Node*& list)
   

7. Given the following expression in postfix notation, what is the result of evaluating it?

   $$ 100 \; 4 \; 5 \; 6 \; + \; * \; - \; 15 \; 3 \; / \;+ $$

8. What gets printed to the standard output when running the following C++ code?

   #include <iostream>
   #include <queue>
   #include <stack>
   
   int main()
   {
       std::stack<int> s;
       std::queue<int> q;
       q.push(4);
       q.push(8);
       q.push(15);
       q.push(16);
       q.push(23);
       q.push(42);
       while (not q.empty()) {
           int x = q.front();
           q.pop();
           if (x % 2 == 0) {
               s.push(x);
           }
       }
       while (not s.empty()) {
           int x = s.top();
           s.pop();
           std::cout << x << " ";
       }
       std::cout << "\n";
       return 0;
   }
   

9. This sorting algorithm uses the fairly obvious fact that, if an array is not sorted, it must contain two adjacent elements that are out of order. The algorithm repeatedly passes through the array, swapping items that are out of order, until it can't find any more swaps. What’s the name of this algorithm?

10. What gets printed to the standard output when running the following C++ code?

    #include <algorithm>
    #include <iostream>
    #include <vector>
    
    bool comparator(int a, int b)
    {
        return std::abs(a) <= std::abs(b);
    }
    
    int main()
    {
        std::vector<int> v {-35, 12, -43, 50, -77, -76, -8, 69};
        std::sort(v.begin(), v.end(), comparator);
        for (int x : v) {
            std::cout << x << " ";
        }
        std::cout << "\n";
        return 0;
    }