Métodos computacionales

Exam: What you need to know

Topics

Part I. Programming Languages and Paradigms

  1. General introduction to Programming Languages ([SCOTT] chapter 1).

    1. Language design.
    2. Classification of programming languages.
    3. Compilation and interpretation.
    4. Overview of compilation.

  2. Clojure fundamentals.

    1. Read, Evaluate, Print, Loop (REPL).
    2. Comments.
    3. Global and local bindings (def, let).
    4. Basic data types (nil, booleans, numbers, strings, characters, symbols, keywords) and their functions: +, +', -, *, *', /, <, <=, =, not=, ==, >, >=, boolean, char, char?, dec, even?, format, inc, keyword?, neg?, nil?, number?, odd?, pos?, quot, rem, str, string?, symbol?, and zero?.
    5. The quote (') special form.
    6. Logic operations: not, and, or. Short-circuit evaluation.
    7. Conditions (if, cond, case). Truthy and falsy values.
    8. Functions. Definition (defn) and application. Parameters. Multi-arity and variadic functions. Docstrings. Anonymous functions and closures. The apply, fn?, and ifn? functions.
    9. Special forms. How they differ from functions.
    10. Repetitions. Recursion and loop/recur.
    11. Functional programming. Higher-order functions.
    12. Destructuring.

  3. Clojure collections.

    1. The concept of sequence.
    2. Sequence functions: butlast, concat, cons, count, cycle, distinct, drop, drop-while, empty?, every?, filter, first, interleave, interpose, iterate, last, map, mapcat, nth, partition, partition-by, range, reduce, remove, repeat, rest, reverse, seq, seq?, some, sort, split-at, split-with, take, and take-while.
    3. Collection types (lists, vectors, maps, and sets).
    4. Lazy sequences.
    5. List functions: conj and list.
    6. Vector functions: assoc, conj, get, nth, vec, and vector.
    7. Map functions: assoc, contains?, dissoc, frequencies, get, keys, merge, vals, and zipmap.
    8. Set functions: conj, contains?, disj, get, and set.

  4. Parallel programming.

    1. Concurrency and parallelism concepts.
    2. Speedup.
    3. Hardware support for parallelism (multiprocessors, SMT, multi-cores).
    4. The pmap function.

Part II. Automata Theory

  1. Finite Automata.

    1. General concepts and terminology (automaton, finite state machine, deterministic and non-deterministic finite automata, alphabet, string, length of string, Kleen star, Kleen plus, language).
    2. Formal definition of a DFA (Deterministic Finite Automaton).
    3. DFA state diagrams.

  2. Regular Expressions.

    1. General concept.
    2. Equivalence between regular expressions and finite automata.
    3. Syntax. Metacharacters. Special escape sequences.
    4. Clojure regular expression functions: re-matches, re-find, and re-seq.

  3. Context-Free Grammars.

    1. General concept.
    2. Formal definition of a CFG (Context-Free Grammar).
    3. CFG derivations and derivation trees.
    4. The instaparse package for building parsers in Clojure.

  4. Turing Machines.

    1. General concept, components and history.
    2. Formal definition of a TM (Turing Machine).
    3. TM terminology: accept, reject, loop infinitely, and halt.
    4. TM state diagrams.
    5. Universal Turing Machine (UTM) and its relation to the von Neumann architecture.

  5. Theory of Computation

    1. Decidable languages (recursive languages). Recognizable languages (recursively enumerable language).
    2. Undecidable problems. Typical examples: Entscheidungsproblem, and the halting problem.
    3. The Church-Turing thesis.
    4. Turing completeness. Examples of Turing-complete and non-Turing-complete languages.
    5. The Chomsky hierarchy. Languages and grammars Type 0, 1, 2, 3.

Allowed Items During the Exam

NOTE: Once the exam starts you are not allowed to share any items with anyone else.

  1. Pen, pencil, eraser, pencil sharpener.

  2. Simple scientific calculator. You are not allowed to use a cell phone, programmable calculator, tablet, computer, or any other electronic device.

  3. Personal cheat sheet with the following characteristics:


    1. Must be one of these:

      • \(5 \times 8\) inches index card (\(12.7 \times 20.32\) cm).

      • Half letter size sheet of paper (\(13.97 \times 21.59\) cm).

    2. Must be handwritten. Computer-made cards/sheets are not allowed.

    3. You can write in both sides of the card/sheet.

    4. Must include your student ID and full name on the upper-left corner of both sides of the card/sheet.

    5. There are no restrictions on the specific content written on the card/sheet.


Sample Questions

  1. Give three examples of Clojure built-in higher-order functions.

  2. What is the result of the following Clojure expression? 

    (take-while #(< % 10)
            (iterate #(+ % %) 1)))

  3. Write a Clojure function called contains-all-digits? that takes an integer argument \(n\) and returns true if \(n\) contains each of the ten digits from 0 to 9 at least once, or false otherwise.

    Examples:

    (contains-all-digits 1023456789)
=> true

(contains-all-digits 1236)
=> false

  4. You are given the following Clojure code: 

    (defn mystery
  ([x] (mystery x #(* 2 %) #(inc %)))
  ([a b c] (c (b a))))

(defn wierd
  [& t]
  (let [n (count t)]
    (cond
      (zero? n) 1
      :else (inc (apply wierd (rest t))))))

    What is the result of evaluating the following expressions?

    1. (mystery 5)
    2. (wierd 4 8 15 16 23 42)
    3. (mystery 2 dec inc)
    4. (mystery 10 wierd (fn [z] (* z z)))

  5. Write a function in Clojure called how-many-div-3 that receives as input a sequence of integers and returns the result of counting how many of these numbers are exactly divisible by 3. For example: 

    (how-many-div-3 ())
=> 0

(how-many-div-3 [6 2 3 12 4])
=> 3

(how-many-div-3 '(2 5 7 11 19))
=> 0

(how-many-div-3 [0 33 66 99])
=> 4

  6. You have a sequential program that takes 10 seconds to execute using 1 processor. The parellel version of the same program takes 2 seconds to execute using 8 processors. Calculate its speedup.

  7. Given \(\Sigma = \{ 0, 1 \} \), you want to define a language \( L \) comprised of all strings that start and end with exactly the same symbol. Thus, these strings belong to this language: 0, 010, 11001010101. Yet, these other strings do not: \( \varepsilon \), 01, 110, 010010011.

    1. Draw a state diagram of a DFA that accepts \( L \).
    2. Write a regular expression that accepts \( L \).
    3. Write a CFG that accepts \( L \).
    4. Draw a state diagram of a TM that accepts \( L \). NOTE: The final position of the tape head is inconsequential.
    5. According to the Chomsky hierarchy, what type of grammar and language is \(L\)?

  8. Write a regular expression that allows valid dates to be recognized using the YYYY-MM-DD format defined in the ISO 8601 standard. The following should be considered to ensure that the vast majority of the recognized dates are valid (although not necessarily all):

    • The year YYYY can range from 0000 to 9999.
    • On month MM the first digit must be 0 or 1. If the first digit is 0, the second must be any digit from 1 to 9. If the first digit is 1, the second digit must be 0, 1 or 2.
    • On day DD the first digit must be 0, 1, 2 or 3. If the first digit is 0, the second must be any digit from 1 to 9. If the first digit is 1 or 2, the second digit must be any digit from 0 to 9. If the first digit is 3, the second digit must be 0 or 1.

    So, for example, the following dates must be recognized by the regular expression:

    • 2023-04-28
    • 1521-08-13
    • 9999-12-31

    However, the following dates should be rejected:

    • 0000-00-00 (there is no month or day 0)
    • 2023-04-32 (there is no day 32)
    • 1998-13-15 (there is no month 13)

  9. How would you explain the Entscheidungsproblem to a smart ten-year-old child?

  10. You have the following state diagram for a Turing machine \(M\):

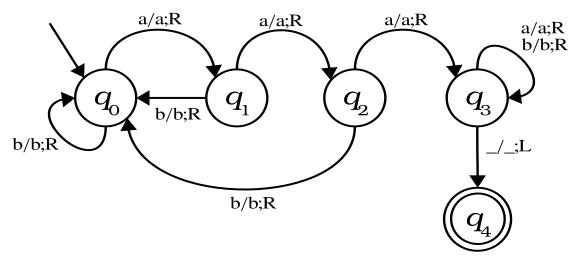
    Remember that, formally, \(M = (Q, \Sigma, \Gamma, \delta, q_0, B, F)\). For the Turing machine above:

    1. What would be the values of \(Q\), \(\Sigma\), \(\Gamma\) and \(F\)?
    2. What would be the shortest input string accepted by \(M\)?
    3. What would be the shortest input string rejected by \(M\)?
    4. Describe in your own words the language accepted by \(M\).
    5. Is there a possibility that \(M\) could enter an infinite loop for a certain finite input? Just answer yes or no. If you answer affirmatively, then indicate an input string that could cause this.

  11. What is the difference between an ordinary Turing machine (TM) and a universal Turing machine (UTM)?

  12. Give two examples of languages used in the software industry. The first language should be Turing-complete, the second should be non-Turing-complete. Justify your answer.