Context-Free Grammars

Introduction

A formal grammar is a set of rules that are used to generate and identify patterns of strings in a language.

Context-Free Grammars (CFGs) are used to describe context-free languages [2]. A CFG can describe all regular languages and more, but they cannot describe all possible languages. A regular language is a language that can be expressed with a regular expression or a DFA/NFA.

CFGs are studied in fields of theoretical computer science, compiler design, and linguistics. They are used to describe programming languages and parser programs in compilers can be generated automatically from CFGs.

Formally, a CFG \(G\) is defined by the 4-tuple \(G = (V,\Sigma ,R,S)\), where [3]:

• \(V\) : The set of nonterminal symbols (or variables). These are the symbols that will always appear on the left-hand side of the production rules, though they can be included on the right-hand side.

• \(\Sigma\) : The set of terminal symbols \((\Sigma \cap V = \varnothing )\) which are the characters that appear in the language/strings generated by the grammar. Terminal symbols never appear on the left-hand side of the production rule and are always on the right-hand side.

• \(R\) : The set of production rules where each production rule maps a variable to a string \(s \in (V \cup \Sigma)^{*}\).

• \(S\) : The start symbol \((S \in V)\) which is a special nonterminal symbol that is used to represent the whole sentence (or program).

Deriving a String from a CFG

Follow these steps [1]:

• Begin the string with a start symbol.
• Apply one of the production rules to the start symbol on the left-hand side by replacing the start symbol with the right-hand side of the production.
• Repeat the process of selecting nonterminal symbols in the string, and replacing them with the right-hand side of some corresponding production, until all nonterminals have been replaced by terminal symbols. Note, it could be that not all production rules are used.

CFG Example

We want a CFG that generates the language \(\{ a^n b^n \; | \; n \ge 0 \}\). In other words, we want to accept strings that contain a sequence of symbols a followed by the exact same number of symbols b.

The formal definition of the CFG that solves this problem is as follows:

• \(V = \{ A \}\)
• \(\Sigma = \{ a, b \}\)
• \(R\) (production rules):
1. \(A \to aAb\)
2. \(A \to \varepsilon\)
• \(S = A\)

NOTE: The above production rules can also be written as: \(A \to aAb \; | \; \varepsilon\)

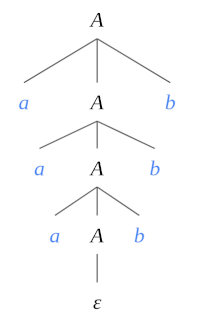
Let’s now verify the following derivation: \(S \stackrel{*}{\Rightarrow} aaabbb\)

$$ \begin{align*} S &\Rightarrow \underline{ A } & \\ &\Rightarrow a \underline{ A } b & (\textrm{result of applying rule 1}) \\ &\Rightarrow a a \underline{ A } b b & (\textrm{result of applying rule 1}) \\ &\Rightarrow a a a \underline{ A } b b b & (\textrm{result of applying rule 1}) \\ &\Rightarrow a a a \varepsilon b b b & (\textrm{result of applying rule 2}) \\ &\Rightarrow a a a b b b & \\ \end{align*} $$

The following derivation tree is an alternative way of generating the desired string:

Instaparse: A Parse Generator

In Clojure, we can use the Instaparse package to create a parser from a CFG.

First, we must import the required dependencies and define some auxilary functions:

(ns instaparse-example
  (:require [instaparse.core :refer [parser]])
  (:import (instaparse.gll Failure)))

(defn fails? [r] (instance? Failure r))
(defn succeeds? [r] (not (fails? r)))

Given a grammar, turning it into an executable parser is as simple as typing the grammar. Using the grammar from the previous example:

(def example (parser "A = 'a' A 'b' | epsilon"))

The parser object behaves like a function that returns the corresponding derivation tree when applied with an input string as argument:

(example "aaabbb")
⇒ [:A "a" [:A "a" [:A "a" [:A] "b"] "b"] "b"]

If the provided string is not syntactically correct it returns an instaparse.gll.Failure object that shows the corresponding error message when displayed:

(example "aaabb")

Parse error at line 1, column 6:
aaabb
     ^
Expected:
"b" (followed by end-of-string)

References

• [1] Brilliant.org Context Free Grammars.
  Retrieved from: https://brilliant.org/wiki/context-free-grammars/

• [2] Hopcroft, John; Motwani, Rajeev; Ullman, Jeffrey. Introduction to Automata Theory, Languages, and Computation, 3rd. Edition. Pearson Education, 2007. ISBN: 9780321455369

• [3] Tutorials Point. Automata Theory Tutorial.
  Retrieved from: https://www.tutorialspoint.com/automata_theory/