Métodos computacionales

Proyecto: Simulador y ensamblador de una máquina de Von Neumann

Objetivo

Durante esta actividad, los alumnos serán capaces de:


Subcompetencias a demostrar con esta evidencia

Competencia Subcompetencia
y nivel de dominio
STC0100:
Desarrollo de algoritmos computacionales

Soluciona problemas generando algoritmos computacionales eficientes bajo modelos y herramientas de las ciencias computacionales.

STC0101A:
Implementación de algoritmos computacionales

Implementa algoritmos computacionales confiables y correctos que solucionan problemas.

STC0102A:
Optimización de algoritmos computacionales

Optimiza algoritmos computacionales robustos y eficientes que se aplican en el desarrollo de soluciones.

STC0103A:
Generación de modelos computacionales

Genera modelos computacionales verificables y correctos para la solución de problemas.

STC0104A:
Implementación de modelos computacionales

Implementa modelos computacionales en la solución de un problema que permiten su interoperatividad con otros modelos.


Introducción

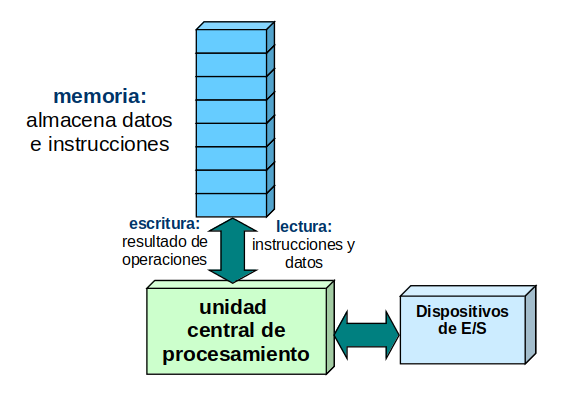
Dentro de una computadora Von Neumann, los datos y el código se almacenan juntos en la misma memoria. La unidad central de procesamiento (CPU), que está a cargo de ejecutar las instrucciones del programa, está separada de la memoria. Por lo tanto, las instrucciones deben trasladarse de la memoria a la CPU. Los resultados de la operación de la CPU deben enviarse de vuelta a la memoria.

Descripción del proyecto

En los equipos ya conformados y utilizando el lenguaje de programación Clojure, realizar en orden la Parte 1 y Parte 2, detalladas a continuación. En una actividad posterior (Video documental) deberán presentar y documentar sus resultados.

Tanto el código de la parte 1 como el de la parte 2 deben ir en un solo archivo fuente llamado proyecto_integrador.clj.

Parte 1: Simulador

Programar un simulador de una máquina con arquitectura de Von Neumann que conste de dos registros (el contador de programa \(\textit{pc}\) y el apuntador de pila \(\textit{sp}\)) y una cantidad arbitraria de palabras de memoria. El apuntador de pila es una parte medular del simulador que le permite funcionar como una máquina de pila.

La máquina debe ser programable usando los códigos de operación (opcodes) descritos en la tabla correspondiente. Cada código de operación se almacena en una palabra de memoria. Si el código de operación requiere un operando, este se debe encontrar en la dirección de palabra inmediata siguiente.

Todas las operaciones aritméticas y de comparación deben utilizar números enteros con signo. Al inicio de la ejecución de un programa el contador del programa (\(\textit{pc}\)) debe ser igual a cero y el apuntador de la pila (\(\textit{sp}\)) debe apuntar a la última dirección de la palabra de memoria + 1.

La función principal del simulador, la cual se debe llamar execute, debe recibir dos entradas: un vector con los opcodes del programa a ejecutar y el tamaño total de la memoria a asignarle a dicho programa. Su valor de regreso debe ser siempre nil si el programa de entrada efectivamente termina. El comportamiento del programa se debe poder observar a partir de la salida producida.

La función execute debe pasar todas las pruebas unitarias del archivo test_execute.clj.

Tabla de Opcodes
Opcode Operation Description New Register Values
\(\textit{pc}\) \(\textit{sp}\)
$$ \texttt{0} $$ $$ \texttt{hlt} $$ Halt. Stops program execution.
$$ \texttt{1} $$ $$ \texttt{nop} $$ No operation. Do nothing. $$ \textit{pc} \leftarrow \textit{pc} + 1 $$
$$ \texttt{2} $$ $$ \texttt{ld} \; \textit{index} $$ Load. Push to stack value at memory location \(\textit{index}\). $$ \texttt{[}\textit{sp } – 1\texttt{]} \leftarrow \texttt{[[}\textit{pc} + 1\texttt{]]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 2 $$ $$ \textit{sp} \leftarrow \textit{sp} - 1 $$
$$ \texttt{3} $$ $$ \texttt{ldi} $$ Load indirect. Pop \(\textit{index}\) from the stack. Push to the stack the value at memory location \(\textit{index}\). $$ \texttt{[}\textit{sp}\texttt{]} \leftarrow \texttt{[[}\textit{sp}\texttt{]]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$
$$ \texttt{4} $$ $$ \texttt{ct} \; \textit{value} $$ Constant. Push \(\textit{value}\) to the stack. $$ \texttt{[}\textit{sp } – 1\texttt{]} \leftarrow \texttt{[}\textit{pc} + 1\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 2 $$ $$ \textit{sp} \leftarrow \textit{sp} - 1 $$
$$ \texttt{5} $$ $$ \texttt{st} \; \textit{index} $$ Store. Pop a value from the stack and store it at memory location \(\textit{index}\). $$ \texttt{[[}\textit{pc} + 1\texttt{]]} \leftarrow \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 2 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{6} $$ $$ \texttt{sti} $$ Store indirect. Pop \(\textit{index}\) from the stack. Pop \(\textit{value}\) from the stack. Store \(\textit{value}\) at memory location \(\textit{index}\). $$ \texttt{[[}\textit{sp}\texttt{]]} \leftarrow \texttt{[}\textit{sp} + 1\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 2 $$
$$ \texttt{7} $$ $$ \texttt{pop} $$ Pop. Discard top of stack. $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{8} $$ $$ \texttt{swp} $$ Swap. Pop two elements from the stack and push them back in reverse order. $$ \begin{align*} t_1 &\leftarrow \texttt{[}\textit{sp}\texttt{]} \\ t_2 &\leftarrow \texttt{[}\textit{sp} + 1\texttt{]} \\ \texttt{[}\textit{sp}\texttt{]} &\leftarrow t_2\\ \texttt{[}\textit{sp} + 1\texttt{]} &\leftarrow t_1\\ \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$
$$ \texttt{9} $$ $$ \texttt{dup} $$ Duplicate. Pop a value from the stack and push it back twice. $$ \texttt{[}\textit{sp} - 1\texttt{]} \leftarrow \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} - 1 $$
$$ \texttt{10} $$ $$ \texttt{add} $$ Add. Pop \(b\) and pop \(a\) from the stack. Push \((a + b)\). $$ \texttt{[}\textit{sp} + 1\texttt{]} \leftarrow \texttt{[}\textit{sp} + 1\texttt{]} + \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{11} $$ $$ \texttt{sub} $$ Subtract. Pop \(b\) and pop \(a\) from the stack. Push \((a - b)\). $$ \texttt{[}\textit{sp} + 1\texttt{]} \leftarrow \texttt{[}\textit{sp} + 1\texttt{]} - \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{12} $$ $$ \texttt{mul} $$ Multiply. Pop \(b\) and pop \(a\) from the stack. Push \((a \times b)\). $$ \texttt{[}\textit{sp} + 1\texttt{]} \leftarrow \texttt{[}\textit{sp} + 1\texttt{]} \times \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{13} $$ $$ \texttt{div} $$ Divide. Pop \(b\) and pop \(a\) from the stack. Push \((a \div b)\). The \(\div\) operation is the integer division, also known as quotient. $$ \texttt{[}\textit{sp} + 1\texttt{]} \leftarrow \texttt{[}\textit{sp} + 1\texttt{]} \div \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{14} $$ $$ \texttt{rem} $$ Remainder. Pop \(b\) and pop \(a\) from the stack. Push \((a \; \texttt{rem} \; b)\). The \(\texttt{rem}\) operation is the remainder of the integer division. $$ \texttt{[}\textit{sp} + 1\texttt{]} \leftarrow \texttt{[}\textit{sp} + 1\texttt{]} \; \texttt{rem} \; \texttt{[}\textit{sp}\texttt{]} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{15} $$ $$ \texttt{eqz} $$ Equal to zero. Pop the top of the stack and if the value is equal to zero push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} \texttt{]} = 0 \\ & \; \; \; \; \texttt{[} \textit{sp} \texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} \texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$
$$ \texttt{16} $$ $$ \texttt{ceq} $$ Compare equal. Pop \(b\) and pop \(a\) from the stack. If \(a = b\) push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} + 1\texttt{]} = \texttt{[} \textit{sp} \texttt{]} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{17} $$ $$ \texttt{cne} $$ Compare not equal. Pop \(b\) and pop \(a\) from the stack. If \(a \ne b\) push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} + 1\texttt{]} \ne \texttt{[} \textit{sp} \texttt{]} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{18} $$ $$ \texttt{clt} $$ Compare less than. Pop \(b\) and pop \(a\) from the stack. If \(a < b\) push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} + 1\texttt{]} < \texttt{[} \textit{sp} \texttt{]} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{19} $$ $$ \texttt{cle} $$ Compare less or equal. Pop \(b\) and pop \(a\) from the stack. If \(a \le b\) push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} + 1\texttt{]} \le \texttt{[} \textit{sp} \texttt{]} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{20} $$ $$ \texttt{cgt} $$ Compare greater than. Pop \(b\) and pop \(a\) from the stack. If \(a > b\) push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} + 1\texttt{]} > \texttt{[} \textit{sp} \texttt{]} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{21} $$ $$ \texttt{cge} $$ Compare greater or equal. Pop \(b\) and pop \(a\) from the stack. If \(a \ge b\) push 1, otherwise push 0. $$ \begin{align*} &\texttt{if [} \textit{sp} + 1\texttt{]} \ge \texttt{[} \textit{sp} \texttt{]} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 1 \\ &\texttt{else} \\ & \; \; \; \; \texttt{[} \textit{sp} + 1\texttt{]} \leftarrow 0 \end{align*} $$ $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{22} $$ $$ \texttt{jp} \; \textit{index} $$ Jump. Continue program execution at the instruction contained at memory location \(\textit{index}\). $$ \textit{pc} \leftarrow \texttt{[} \textit{pc} + 1 \texttt{]} $$
$$ \texttt{23} $$ $$ \texttt{jpc} \; \textit{index} $$ Jump conditional. Pop a value from the stack and if it’s not equal to zero continue program execution at the instruction contained at memory location \(\textit{index}\), otherwise continue with next instruction. $$ \begin{align*} &\texttt{if [} \textit{sp}\texttt{]} \ne 0 \\ & \; \; \; \; \textit{pc} \leftarrow \texttt{[} \textit{pc} + 1\texttt{]} \\ &\texttt{else} \\ & \; \; \; \; \textit{pc} \leftarrow \textit{pc} + 2 \end{align*} $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{24} $$ $$ \texttt{jpi} $$ Jump indirect. Pop \(\textit{index}\) from the stack. Continue program execution at the instruction contained at memory location \(\textit{index}\). $$ \textit{pc} \leftarrow \texttt{[} \textit{sp}\texttt{]} $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{25} $$ $$ \texttt{out} $$ Output. Pop a value from the stack and print it on the standard output followed by a single space. $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$
$$ \texttt{26} $$ $$ \texttt{chr} $$ Character. Pop \(\textit{value}\) from the stack. Print to the standard output the character with a Unicode code point equal to \(\textit{value}\). No space is added afterwards. $$ \textit{pc} \leftarrow \textit{pc} + 1 $$ $$ \textit{sp} \leftarrow \textit{sp} + 1 $$

Parte 2: Ensamblador

Escribir un programa ensamblador para la máquina de Von Neumann desarrollada en la parte 1. Es importante considerar los siguientes aspectos:

Ejemplo

Sea factorial.von un archivo de texto con el siguiente contenido: 

; Calcular e imprimir el factorial de n

label inicio_ciclo

    ;;; Terminar ciclo si: i > n
    ld i
    ld n
    cgt
    jpc salir_ciclo

    ;;; r = r * i
    ld r
    ld i
    mul
    st r

    ;;; i++
    ld i
    ct 1
    add
    st i

    jp inicio_ciclo

label salir_ciclo

    ;;; Imprimir r
    ld r
    out

    ;;; Terminar programa
    hlt

;;; Sección de datos
label n data 5
label r data 1
label i data 1

La función que realiza el ensamblado del archivo anterior debe producir el siguiente vector de Clojure: 

[2 29 2 27 20 23 23 2 28 2 29 12 5 28
 2 29 4 1 10 5 29 22 0 2 28 25 0 5 1 1]

NOTA: La salida del ensamblador debe servir como entrada para el simulador de la máquina de Von Neumann.

El programa anterior debe imprimir 120 al ejecutar los opcodes contenidos en el vector.

Programas de Prueba

¿Qué se debe entregar?

Todo el código de Clojure del proyecto debe seguir las convenciones de codificación descritas en The Clojure Style Guide.

El archivo fuente del programa debe incluir en la parte superior los datos personales de los autores (matrícula y nombre) dentro de comentarios. Por ejemplo: 

;----------------------------------------------------------
; Proyecto integrador: Simulador y ensamblador de una
; máquina de Von Neumann
; Fecha: 15 de junio, 2022.
; Autores:
;          A01770771 Sylvie Laufeydottir
;          A01777771 Loki Laufeyson
;----------------------------------------------------------

Además, cada función debe incluir una cadena de documentación (docstring) con una breve descripción de su comportamiento. Por ejemplo: 

(defn max2
  "Devuelve el mayor de los dos números x e y."
  [x y]
  (if (> x y) x y))

Instrucciones para subir archivo

Para entregar el archivo proyecto_integrador.clj, ingresa los siguientes datos:

Solicitar NIP

Solo es necesario que lo entregue un miembro del equipo.

La fecha límite es el jueves 16 de junio.

Evaluación

Esta actividad será evaluada utilizando los siguientes criterios:

-10 El programa no contiene dentro de comentarios la información personal de los autores.
-20 Falta una cadena de documentación en una o más funciones.
-30 No se utilizan consistentemente las convenciones de codificación detalladas en The Clojure Style Guide.
10 El programa no se puede correr porque tiene errores de sintaxis o de otro tipo.
1 El programa fue plagiado parcial o totalmente.
10-100 Dependiendo de la funcionalidad correctamente implementada.