Problem Set #9: Turing Machines

Objective

During this activity, students should be able to:

Design and implement simulations of Turing machines (TM).

This activity helps students develop the following skills, values and attitudes: ability to analyze and synthesize, capacity for identifying and solving problems, and efficient use of computer systems.

Activity Description

Solve with your team the Clojure exercises described in this problem set. Make sure the code passes all the unit tests.

Create a namespace called turing-machines. At the begining of the file add the following code in order to declare the namespace and import the required external functions:

(ns turing-machines
  (:require [clojure.test :refer [deftest is run-tests]]))

and at the end add:

(run-tests)

All the code you write should go between these two instructions.

Implement a Turing machine (TM) simulator. In order to do this, write a function called accepts that takes two arguments: $\textit{tm}$ and $\textit{input}$, where $\textit{tm}$ is an object that holds the information associated to a Turing machine (start state, set of accepting states, transition function), and $\textit{input}$ is a string with a sequence of symbols that belong to $\Sigma$. The function returns a string with the final contents of the tape if $\textit{input}$ is accepted by $\textit{tm}$ or nil if it is rejected.

Note that the tape head is included as part of the result and is represented by using square brackets to enclose the symbol contained in the current cell being scanned (for example: "aaaaaaa[a]"). Blank symbols are represented with an underscore character ( _ ), but are excluded from the result when they occur at the beginning or at the end of the result (for example: "xxx[_]" instead of "___xxx[_]__").

Test the function with a TM that accepts the language $\{ a^n \; | \; n \ge 0, n \bmod 2 = 0\}$. This is the state diagram for this TM:

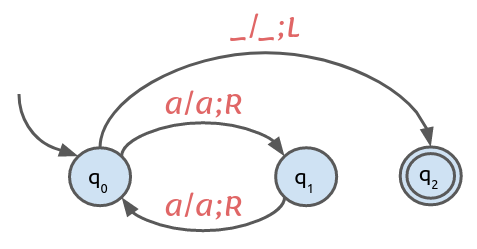
For the following unit tests, tm-1 is assumed to be the binding to the corresponing Turing machine object. Note that, on an accepted input, the string returned must have the tape head over the rightmost nonblank symbol, if any.
```
(deftest test-problem1
  (is (= "[_]"
         (accepts tm-1 "")))
  (is (= "a[a]"
         (accepts tm-1 "aa")))
  (is (= "aaaaaaa[a]"
         (accepts tm-1 "aaaaaaaa")))
  (is (= "aaaaaaaaaaaaaaaaaaaaaaaaa[a]"
         (accepts tm-1 "aaaaaaaaaaaaaaaaaaaaaaaaaa")))
  (is (nil? (accepts tm-1 "a")))
  (is (nil? (accepts tm-1 "aaa")))
  (is (nil? (accepts tm-1 "aaaaaaa")))
  (is (nil? (accepts tm-1 "aaaaaaaaaaaaaaaaaaaaaaaaa"))))
```

Design and code a TM called tm-2 with $\Sigma = \{0, 1\}$ that remembers the first symbol that it sees and checks that it does not appear elsewhere on its input. Note that on an accepted input, the string returned must have the tape head over the rightmost nonblank symbol.

Unit tests:

(deftest test-problem2
  (is (= "[0]"
         (accepts tm-2 "0")))
  (is (= "[1]"
         (accepts tm-2 "1")))
  (is (= "1[0]"
         (accepts tm-2 "10")))
  (is (= "0111111111[1]"
         (accepts tm-2 "01111111111")))
  (is (nil? (accepts tm-2 "")))
  (is (nil? (accepts tm-2 "00")))
  (is (nil? (accepts tm-2 "100000000001")))
  (is (nil? (accepts tm-2 "10011010100101011"))))

Given $\Sigma = \{0, 1\}$, design and code a TM called tm-3 that increments by one the binary number contained in the input tape. Note that the string returned must have the tape head over the rightmost nonblank symbol.

Unit tests:

(deftest test-problem3
  (is (= "[1]"
         (accepts tm-3 "0")))
  (is (= "1[0]"
         (accepts tm-3 "1")))
  (is (= "1[1]"
         (accepts tm-3 "10")))
  (is (= "10[0]"
         (accepts tm-3 "11")))
  (is (= "100[1]"
         (accepts tm-3 "1000")))
  (is (= "10101011[0]"
         (accepts tm-3 "101010101")))
  (is (= "000000000[1]"
         (accepts tm-3 "0000000000")))
  (is (= "11111000[0]"
         (accepts tm-3 "111101111")))
  (is (= "101001101[1]"
         (accepts tm-3 "1010011010")))
  (is (= "1000000000000000[0]"
         (accepts tm-3 "1111111111111111"))))

The monus of two positive integers $m$ and $n$, also known as proper subtraction, is defined as:

$m$ ∸ $n = \max(m - n, 0)$

That is, $m$ ∸ $n$ is $m - n$ if $m \ge n $ and 0 if $m < n $.

Given $\Sigma = \{a, $\}$, design and code a TM called tm-4 that implements the monus operation. The machine starts with a tape consisting of $a^m$a^n$ $(m, n \ge 0)$ and halts with $a$^{$m$ ∸ $n$} on its tape . Note that the string returned must have the tape head over the rightmost nonblank symbol, if any.

Unit tests:

(deftest test-problem4
  (is (= "[_]"
         (accepts tm-4 "$")))
  (is (= "[_]"
         (accepts tm-4 "a$a")))
  (is (= "[a]"
         (accepts tm-4 "aa$a")))
  (is (= "aa[a]"
         (accepts tm-4 "aaaaa$aa")))
  (is (= "[_]"
         (accepts tm-4 "aaaaa$aaaaaaaa")))
  (is (= "aa[a]"
         (accepts tm-4 "aaaaaaaa$aaaaa")))
  (is (= "[_]"
         (accepts tm-4 "$aaaaaaaaaaaaa")))
  (is (= "aaaaaaaaaaaa[a]"
         (accepts tm-4 "aaaaaaaaaaaaa$"))))

Given $\Sigma = \{a, b, c\}$, design and code a TM called tm-5 that accepts the language $\{ a^n b^n c^n \; | \; n \ge 0 \}$. The contents of the tape may be discarded.

Unit tests:

(deftest test-problem5
  (is (accepts tm-5 ""))
  (is (accepts tm-5 "abc"))
  (is (accepts tm-5 "aaabbbccc"))
  (is (accepts tm-5 "aaaaaaaaaabbbbbbbbbbcccccccccc"))
  (is (nil? (accepts tm-5 "a")))
  (is (nil? (accepts tm-5 "aabbc")))
  (is (nil? (accepts tm-5 "aabaca")))
  (is (nil? (accepts tm-5 "cccaaabbb")))
  (is (nil? (accepts tm-5 "aaaaaccccc")))
  (is (nil? (accepts tm-5 "abcabcabcabc")))
  (is (nil? (accepts tm-5 "aaaaabbbbbcccccc")))
  (is (nil? (accepts tm-5 "aaaaaaaaaabbbbbbbbbcccccccccc"))))

Given $\Sigma = \{0, 1\}$, design and code a TM called tm-6 that accepts any string that has an equal number of $0$’s and $1$’s. The contents of the tape may be discarded.

Unit tests:

(deftest test-problem6
  (is (accepts tm-6 ""))
  (is (accepts tm-6 "01"))
  (is (accepts tm-6 "10"))
  (is (accepts tm-6 "11000101"))
  (is (accepts tm-6 "1010011010"))
  (is (accepts tm-6 "1010101010101010"))
  (is (accepts tm-6 "1111111100000000"))
  (is (accepts tm-6 "00000111111111100000"))
  (is (nil? (accepts tm-6 "11")))
  (is (nil? (accepts tm-6 "01010")))
  (is (nil? (accepts tm-6 "11111111000000001")))
  (is (nil? (accepts tm-6 "10101111001101110101")))
  (is (nil? (accepts tm-6 "000000000000000000000")))
  (is (nil? (accepts tm-6 "11111111110111111111111"))))