Concurrency and Parallelism

Introduction

A program is said to be concurrent if it may have more than one active execution context. In other words, it has more than one “thread of control”.

Concurrency has at least three important motivations:

To capture the logical structure of a problem. Many programs, particularly servers and graphical applications, must keep track of more than one largely independent “task” at the same time. Often the simplest and most logical way to structure such a program is to represent each task with a separate thread of control.
To exploit extra processors, for speed. Long a staple of high-end servers and supercomputers, multiple processors have recently become ubiquitous in desktop and laptop machines. To use them effectively, programs must generally be written (or rewritten) with concurrency in mind.
To cope with separate physical devices. Applications that run across the Internet or a more local group of machines are inherently concurrent. Likewise, many embedded applications―the control systems of a modern automobile, for example―often have separate processors for each of several devices.

In general, we use the word concurrent to characterize any system in which two or more tasks may be underway (at an unpredictable point in their execution) at the same time. Under this definition, coroutines are not concurrent, because at any given time, all but one of them is stopped at a well-known place. A concurrent system is parallel if more than one task can be physically active at once; this requires more than one processor. The distinction is purely an implementation and performance issue: from a semantic point of view, there is no difference between true parallelism and the “quasiparallelism” of a system that switches between tasks at unpredictable times. A parallel system is distributed if its processors are associated with people or devices that are physically separated from one another in the real world. Under these definitions, “concurrent” applies to all three motivations above. “Parallel” applies to the second and third; “distributed” applies to only the third.

Speedup

The speed of a program is the time it takes the program to execute. This could be measured in any increment of time. Speedup is defined as the time it takes a program to execute sequentially (with one processor) divided by the time it takes to execute in parallel (with many processors). The formula for speedup is:

$$ S_p = \frac{T_1}{T_p} $$

where:

$S_p$ is the speedup obtained from using $p$ processors.
$T_1$ is the time it takes the program to be executed sequentially using 1 processor.
$T_p$ is the time it takes the program to be executed in parallel using $p$ processors.

Linear Speedup

Linear speedup or ideal speedup is obtained when:

$$ S_p = p $$

When running an algorithm with linear speedup, doubling the number of processors doubles the speed. As this is ideal, it is considered very good scalability.

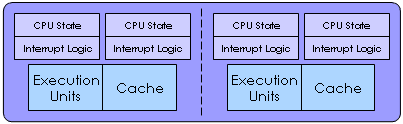
Microprocessor Comparison

Microprocessor	Diagram
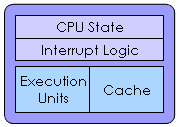
Single Core
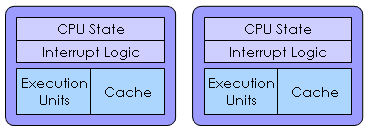
Multiprocessor
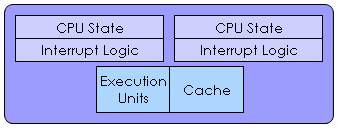
Simultaneous Multithreading (SMT)
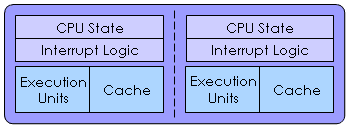
Multi-Core
Multi-Core with Simultaneous Multithreading (SMT)

References

[SCOTT] pp. 575 & 576.
[AKHTER] pp. 9-15.