Métodos computacionales

Chomsky Hierarchy

American linguist Noam Chomsky defined in 1956 a classification of languages in terms of four levels of complexity. This four-level hierarchy, called the Chomsky hierarchy, corresponds to four classes of machines [1].

The following table summarizes each of Chomsky's four types of grammars, the class of language it generates, and the type of machine that recognizes it.

Grammar Language Machine
Type 0
Unrestricted
grammar 		\(L_{\texttt{RE}}\)
Recursively enumerable language		 Turing machine (TM)
Type 1
Context-sensitive
grammar 		\(L_{\texttt{CS}}\)
Context-sensitive language		 Linear-bounded automaton (LBA)
Type 2
Context-free
grammar 		\(L_{\texttt{CF}}\)
Context-free language		 Pushdown automaton (PDA)
Type 3
Regular
grammar 		\(L_{\texttt{Reg}}\)
Regular language		 Finite automaton (DFA/NFA)

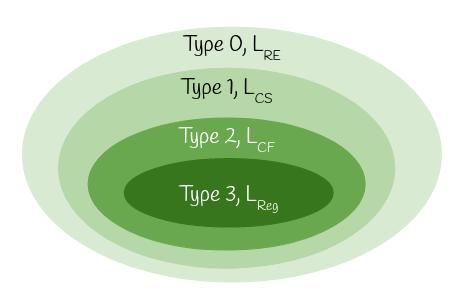
Each language of type \(i\) is a proper subset of the family of type \(i − 1\). The following diagram exhibits the relationship clearly:

Reference