Práctica 7: Fork/Join
Objetivos
Durante esta actividad, los alumnos serán capaces de:
- Resolver diferentes problemas que involucren el uso del API de Fork/Join de Java para paralelizar algoritmos recursivos con el fin de hacer que se ejecuten de manera más veloz.
Esta actividad promueve las siguientes habilidades, valores y actitudes: análisis y síntesis, capacidad de resolver problemas, creatividad, y uso eficiente de la informática y las telecomunicaciones.
Descripción
Esta actividad puede ser elaborada de manera individual o en parejas.
Bibliografía
Peter Pacheco.
An Introduction to Parallel Programming.
Morgan Kaufmann, 2011. pp. 267 y 268.
ISBN: 0123742609
-
Supongamos que lanzamos dardos al azar a un tablero cuadrado, que mide dos metros de cada lado l, y que contiene un círculo que mide un metro de radio r, tal como se muestra en la siguiente figura:
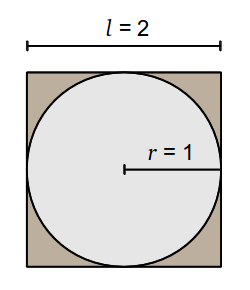
El área del cuadrado es l × l = 2 × 2 = 4, mientras que el área del círculo es π × r 2 = π × 12 = π. Si los puntos en los que caen los dardos están distribuidos de manera uniforme (y siempre dentro del cuadrado), entonces se cumple aproximadamente con la siguiente relación:
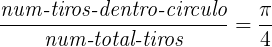
Podemos utilizar esta fórmula para estimar el valor de pi utilizando un generador de número aleatorios:
public static double sequentialMonteCarlo(int n) { Random rnd = new Random(); int sum = 0; for (int i = 0; i < n; i++) { // Generar dos números aleatorios entre -1 y 1. double x = rnd.nextDouble() * 2 - 1; double y = rnd.nextDouble() * 2 - 1; // Aplicar teorema de Pitágoras. double h = x * x + y * y; // Verificar si el tiro cayó dentro del círculo. if (h <= 1) { sum++; } } return 4 * ((double) sum / n); }
A este algoritmo se le llama método de “Monte Carlo” debido a que involucra eventos aleatorios (los tiros de dardos).
Crea el archivo
MonteCarloTask.javay escribe en éste una clase llamadamx.itesm.cem.forkjoin.MonteCarloTask, la cual debe heredar de la clasejava.util.concurrent.RecursiveTask<V>, con el fin de paralelizar el problema anterior.Prueba tu código con el archivo MonteCarlo.java. La salida esperada al ejecutar el programa en un sistema con cuatro núcleos físicos (y ocho núcleos lógicos) debe ser similar a la siguiente (los resultados y tiempos pueden variar):
Resultado secuencial = 3.141670 Ts = 3.82 seg. Resultado paralelo = 3.141802 Tp = 0.85 seg. Sp = Ts/Tp = 4.4745
NOTA: Puedes considerar que tu programa está correctamente implementado si el resultado paralelo es cercano a 3.14 y si Sp > 1. -
Count Sort (ordenamiento por conteo) es un algoritmo de ordenamiento que puede ser implementado de manera secuencial como se muestra a continuación:
public static void sequentialCountSort(int a[]) { final int n = a.length; final int[] temp = new int[n]; for (int i = 0; i < n; i++) { int count = 0; for (int j = 0; j < n; j++) { if (a[j] < a[i]) { count++; } else if (a[i] == a[j] && j < i) { count++; } } temp[count] = a[i]; } System.arraycopy(temp, 0, a, 0, n); }
Para cada elemento
a[i]del arregloa, contamos el número de elementos del arreglo que son menores aa[i]. Posteriormente insertamosa[i]a un arreglo temporal usando como índice el resultado del conteo correspondiente. Solo hay un pequeño detalle que cuidar, ya que si hay elementos repetidos en el arregloaéstos ocuparían la misma localidad dentro del arreglo temporal. Pare evitar este problema, el código incrementa el contador para elementos iguales en base a sus índices. Es decir, sia[i] == a[j]yj < i, entonces consideramos aa[j]como “menor que”a[i].Una vez que concluye el algoritmo, sobre-escribimos el arreglo original con el contenido del arreglo temporal usando el método
System.arraycopy().Crea el archivo
CountSortAction.javay escribe en éste una clase llamadaemx.itesm.cem.forkjoin.CountSortAction, la cual debe heredar de la clasejava.util.concurrent.RecursiveAction, con el fin de paralelizar el problema anterior.Prueba tu código con el archivo CountSort.java. La salida esperada al ejecutar el programa en un sistema con cuatro núcleos físicos (y ocho núcleos lógicos) debe ser similar a la siguiente (los tiempos pueden variar):
Antes de ordenamiento secuencial, arreglo ordenado: false Después de ordenamiento secuencial, arreglo ordenado: true Ts = 22.81 seg. Antes de ordenamiento paralelo, arreglo ordenado: false Después de ordenamiento paralelo, arreglo ordenado: true Tp = 4.36 seg. Sp = Ts/Tp = 5.2323
NOTA: Puedes considerar que tu programa está correctamente implementado si el ordenamiento paralelo deja al arreglo ordenado y si Sp > 1.
¿Qué se debe entregar?
Tus dos archivos fuente de Java deben comenzar con un comentario que contenga el título de la práctica, la fecha y los datos personales de los autores (nombre y matrícula). Por ejemplo:
/*---------------------------------------------------------- * Práctica 7: Fork/Join * Fecha: 23-Abr-2018 * Autores: * A01166611 Pepper Pots * A01160611 Anthony Stark *----------------------------------------------------------*/
Coloca los dos archivos MonteCarloTask.java y CountSortAction.java dentro de un archivo ZIP llamado practica7.zip.
Instrucciones para subir archivo
Para entregar el archivo practica7.zip, ingresa los siguientes datos:
Si la práctica fue desarrollada en pareja, basta que solo uno de los miembros la entregue.
La fecha límite es el lunes 23 de abril.
Evaluación
Esta actividad será evaluada usando los siguientes criterios:
| -10 | No se incluyó en comentario los datos de los autores. |
|---|---|
| 10-100 | Dependiendo del número de métodos correctamente implementados. |
| 10 | El programa no compila. |
| 1 | El programa es un plagio total o parcial. |