Método de Monte Carlo

Supongamos que lanzamos dardos al azar a un tablero cuadrado que mide dos metros de cada lado l, y que contiene un círculo que mide un metro de radio r, tal como se muestra en la siguiente figura:

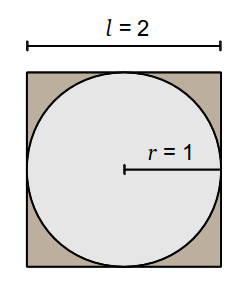
El área del cuadrado es l × l = 2 × 2 = 4, mientras que el área del círculo es π × r ² = π × 1² = π. Si los puntos en los que caen los dardos están distribuidos de manera uniforme (y siempre dentro del cuadrado), entonces se cumple aproximadamente con la siguiente relación:

Podemos utilizar esta fórmula para estimar el valor de pi utilizando un generador de número aleatorios. El código secuencial en Java se vería así:

public static double sequentialMonteCarlo(int n) {
    int sum = 0;
    for (int i = 0; i < n; i++) {
        // Generar dos números aleatorios entre -1 y 1.
        double x = ThreadLocalRandom.current().nextDouble() * 2 - 1;
        double y = ThreadLocalRandom.current().nextDouble() * 2 - 1;

        // Aplicar teorema de Pitágoras.
        double h = x * x + y * y;

        // Verificar si el tiro cayó dentro del círculo.
        if (h <= 1) {
            sum++;
        }
    }
    return 4 * ((double) sum / n);
}

A este algoritmo se le llama método de “Monte Carlo” debido a que involucra eventos aleatorios (los tiros de dardos).

Reference: [PACHECO] pp. 267 y 268.

Programación multinúcleo

Método de Monte Carlo