

During this activity, students should be able to:
This activity helps the student develop the following skills, values and attitudes: ability to analyze and synthesize, capacity for identifying and solving problems, and efficient use of computer systems.
Individually or in pairs, solve the following set of programming exercises using Clojure. Place all your functions in a file called higherorder.clj.
NOTE: The tests in problems 3 and 4 require comparing floating point numbers. In order to avoid rounding problems, we need to define the following function called aprox=:
(defn aprox= "Checks if x is approximately equal to y. Returns true if |x - y| < epsilon, or false otherwise." [epsilon x y] (< (Math/abs (- x y)) epsilon))
my-map-indexed takes two arguments: a function f and a list lst. It returns a list consisting of the result of applying f to 0 and the first item of lst, followed by applying f to 1 and the second item in lst, and so on until lst is exhausted. Function f should accept 2 arguments: index and item. Do not use the predefined map-indexed function. Unit tests:
(deftest test-my-map-indexed (is (= () (my-map-indexed vector ()))) (is (= '([0 a] [1 b] [2 c] [3 d]) (my-map-indexed vector '(a b c d)))) (is (= '(10 4 -2 8 5 5 13) (my-map-indexed + '(10 3 -4 5 1 0 7)))) (is (= '(0 1 -4 3 1 0 6) (my-map-indexed min '(10 3 -4 5 1 0 7)))))
my-drop-while takes two arguments: a function f and a list lst. It returns a list of items from lst dropping the initial items that evaluate to true when passed to f. Once a false value is encountered, the rest of the list is returned. Function f should accept one argument. Do not use the predefined drop-while function. Unit tests:
(deftest test-my-drop-while (is (= () (my-drop-while neg? ()))) (is (= '(0 1 2 3 4) (my-drop-while neg? '(-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4)))) (is (= '(2 three 4 five) (my-drop-while symbol? '(zero one 2 three 4 five)))) (is (= '(0 one 2 three 4 five) (my-drop-while symbol? '(0 one 2 three 4 five)))))
The bisection method is a root-finding algorithm which works by repeatedly dividing an interval in half and then selecting the subinterval in which the root exists.
Suppose we want to solve the equation f(x) = 0. Given two points a and b such that f(a) and f(b) have opposite signs, f must have at least one root in the interval [a, b] as long as f is continuous on this interval. The bisection method divides the interval in two by computing c = (a+b) / 2. There are now two possibilities: either f(a) and f(c) have opposite signs, or f(c) and f(b) have opposite signs. The bisection algorithm is then applied to the sub-interval where the sign change occurs.
Write the function bisection, that takes a, b, and f as arguments. It finds the corresponding root using the bisection method. The algorithm must stop when a value of c is found such that:
|f(c)| < 1.0×10-15.
Unit tests:
(deftest test-bisection (is (aprox= 0.0001 3.0 (bisection 1 4 (fn [x] (* (- x 3) (+ x 4)))))) (is (aprox= 0.0001 -4.0 (bisection -5 0 (fn [x] (* (- x 3) (+ x 4)))))) (is (aprox= 0.0001 Math/PI (bisection 1 4 (fn [x] (Math/sin x))))) (is (aprox= 0.0001 (* 2 Math/PI) (bisection 5 10 (fn [x] (Math/sin x))))) (is (aprox= 0.0001 1.618033988749895 (bisection 1 2 (fn [x] (- (* x x) x 1))))) (is (aprox= 0.0001 -0.6180339887498948 (bisection -10 1 (fn [x] (- (* x x) x 1))))))
Use the Math/abs function to compute the absolute value of a number.
The derivate of a function f(x) with respect to variable x is defined as:
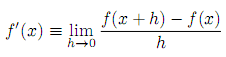
Where f must be a continuous function. Write the
function deriv that takes f and h as its arguments, and returns a new function that takes x as argument, and which represents the derivate of f given a certain value for h.
The unit tests verify the following derivates:
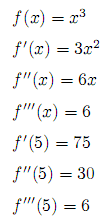
Unit tests:
(defn f [x] (* x x x)) (def df (deriv f 0.001)) (def ddf (deriv df 0.001)) (def dddf (deriv ddf 0.001)) (deftest test-deriv (is (aprox= 0.05 75 (df 5))) (is (aprox= 0.05 30 (ddf 5))) (is (aprox= 0.05 6 (dddf 5))))
Simpson's rule is a method for numeric integration:
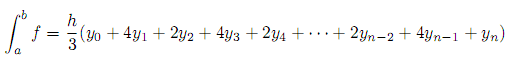
Where n is an even positive integer (if you increment the value of n you get a better approximation), and h and yk are defined as follows:
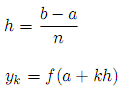
Write the function integral, that takes as arguments a, b, n, and f. It returns the value of the integral, using Simpson's rule. The unit tests verify the following single and double integrals (with n = 10):
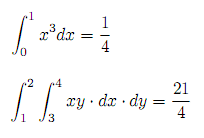
Unit tests:
(deftest test-integral (is (= 1/4 (integral 0 1 10 (fn [x] (* x x x))))) (is (= 21/4 (integral 1 2 10 (fn [x] (integral 3 4 10 (fn [y] (* x y))))))))
Deliver a single file called higherorder.clj containing your solutions and the unit tests. Please provide the following information:
Only one team member needs to upload the file.
IMPORTANT: The program source file must include at the top the authors’ personal information (name and student id) within comments. For example:
;---------------------------------------------------------- ; Activity: Higher-Order Functions ; Date: February 11, 2016. ; Authors: ; A01166611 Pepper Pots ; A01160611 Anthony Stark ;----------------------------------------------------------
Due date is Thursday, February 11.
This activity will be evaluated using the following criteria:
| -10 | The program doesn't contain within comments the author's personal information. |
|---|---|
| 10 | The program contains syntax errors. |
| DA | The program was plagiarized. |
| 10-100 | Depending on the amount of exercises that were solved correctly. |