Loops and Conditionals

Objectives

During this activity, students should be able to:

Write programs using the Python programming language in order to solve problems that involve using functions, for loops, and conditionals.

This activity helps students develop the following skills, values and attitudes: proficiency in English, ability to analyze and synthesize, capacity to identify and solve problems, and efficient use of computer systems.

Activity Description

Individually or in pairs, solve the following set of problems using Python 3.4. Run and test each of your programs to make sure they work as expected.

Each source file must include at the top the authors’ personal information (student ID and name) within comments. For example:

# Authors: 
#          A01166611 Pepper Pots
#          A01160611 Anthony Stark
#
# Description of problem being solved.
#
# February 13, 2015.

    .
    . (The rest of the program goes here)
    .

Write a program powers.py that prints a table of values of n and 2ⁿ for n = 1, 2, 3, ..., 10. You do not need to use any functions other than main().

The program’s output should look like this:
```
1 2
2 4
3 8
4 16
5 32
6 64
7 128
8 256
9 512
10 1024
```

Write a program called table.py that prints a table of values n, log n, n log n, n², and 2ⁿ for n = 10, 20, 30, ..., 200. The log function is in the math module. You do not need to use any functions other than main().

The program’s output should look like this:

10 2.302585092994046 23.02585092994046 100 1024
20 2.995732273553991 59.914645471079815 400 1048576
30 3.4011973816621555 102.03592144986466 900 1073741824
40 3.6888794541139363 147.55517816455745 1600 1099511627776
50 3.912023005428146 195.6011502714073 2500 1125899906842624
60 4.0943445622221 245.66067373332604 3600 1152921504606846976
70 4.248495242049359 297.39466694345515 4900 1180591620717411303424
80 4.382026634673881 350.5621307739105 6400 1208925819614629174706176
90 4.499809670330265 404.9828703297238 8100 1237940039285380274899124224
100 4.605170185988092 460.51701859880916 10000 1267650600228229401496703205376
110 4.700480365792417 517.0528402371658 12100 1298074214633706907132624082305024
120 4.787491742782046 574.4990091338454 14400 1329227995784915872903807060280344576
130 4.867534450455582 632.7794785592257 16900 1361129467683753853853498429727072845824
140 4.941642422609304 691.8299391653026 19600 1393796574908163946345982392040522594123776
150 5.0106352940962555 751.5952941144383 22500 1427247692705959881058285969449495136382746624
160 5.075173815233827 812.0278104374122 25600 1461501637330902918203684832716283019655932542976
170 5.135798437050262 873.0857342985446 28900 1496577676626844588240573268701473812127674924007424
180 5.19295685089021 934.7322331602379 32400 1532495540865888858358347027150309183618739122183602176
190 5.247024072160486 996.9345737104924 36100 1569275433846670190958947355801916604025588861116008628224
200 5.298317366548036 1059.6634733096073 40000 1606938044258990275541962092341162602522202993782792835301376

Write a program temptable.py. The program should contain a function called fahrenheit_to_celsius(x) that converts x degrees Fahrenheit to its equivalent degrees Celsius. Remember that:

°C = (5 / 9)(°F - 32)

The main() function should print a table for temperatures between –30°F and 100°F at 10 degree intervals, with their corresponding conversion to degrees Celsius as returned by the fahrenheit_to_celsius(x) function.

The program’s output should look like this:
```
-30 °F = -34.44444444444444 °C
-20 °F = -28.88888888888889 °C
-10 °F = -23.333333333333332 °C
0 °F = -17.77777777777778 °C
10 °F = -12.222222222222221 °C
20 °F = -6.666666666666667 °C
30 °F = -1.1111111111111112 °C
40 °F = 4.444444444444445 °C
50 °F = 10.0 °C
60 °F = 15.555555555555555 °C
70 °F = 21.11111111111111 °C
80 °F = 26.666666666666668 °C
90 °F = 32.22222222222222 °C
100 °F = 37.77777777777778 °C
```

Write a program disttable.py that prints a table of mile to kilometer conversions for distances between 100 and 1500 miles at 100 mile intervals. Write a function called miles_to_km(x) to do the conversion. One mile is approximately 1.609 km.

The program’s output should look like this:

100 miles = 160.9 km
200 miles = 321.8 km
300 miles = 482.7 km
400 miles = 643.6 km
500 miles = 804.5 km
600 miles = 965.4 km
700 miles = 1126.3 km
800 miles = 1287.2 km
900 miles = 1448.1 km
1000 miles = 1609.0 km
1100 miles = 1769.9 km
1200 miles = 1930.8 km
1300 miles = 2091.7 km
1400 miles = 2252.6 km
1500 miles = 2413.5 km

Write a program called basel.py. Define in this program a function called basel(n) that calculate the following series:

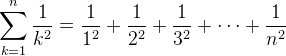
The program’s main() function should print a table with the values of basel(n) for n = 10, 100, 1000, ..., 10⁷. Hint: Use range() to create the exponents.

The program’s output should look like this:
```
10 1.5497677311665408
100 1.6349839001848923
1000 1.6439345666815615
10000 1.6448340718480652
100000 1.6449240668982423
1000000 1.64493306684877
10000000 1.6449339668472596
```
Write a program called pyramid.py. Define in this program a function pyramid(n) that returns 1² + 2²+ 3² + ... + n². The program’s main() function should print a table with the values of pyramid(n) for n = 1, 2, 3, ..., 20.

The program’s output should look like this:
```
1 1
2 5
3 14
4 30
5 55
6 91
7 140
8 204
9 285
10 385
11 506
12 650
13 819
14 1015
15 1240
16 1496
17 1785
18 2109
19 2470
20 2870
```
Write a program called equilateral.py that takes as input the lengths of three sides of a triangle. The program output sould indicate whether or not the triangle is an equilateral. You do not need to use any functions other than main().

Example 1 (user input is in blue):
```
Side 1 of the triangle: 42
Side 2 of the triangle: 42
Side 3 of the triangle: 42
The triangle is an equilateral.
```
Example 2:
```
Side 1 of the triangle: 56
Side 2 of the triangle: 25
Side 3 of the triangle: 43
The triangle is not an equilateral.
```

Write a program called grade.py. Define in this program a function called grade(score) that returns a string with the corresponding letter grade for a given numerical score. Use the values from the following table:

Score	Grade
From 95 to 100	`'A'`
From 85 to 94	`'B'`
From 70 to 84	`'C'`
From 50 to 69	`'D'`
From 0 to 49	`'F'`
Any value less than 0 or greater than 100	`'ERROR'`

The program’s main() function should prompt the user for a score and print the corresponding grade.

Example (user input is in blue):

Give me a score between 0 and 100: 76
The grade is: C

Write a program called max3.py. Define in this program a function called max3(x, y, z) that returns the largest of x, y, and z. Do not use the built-in Python function max(). The program’s main() function should prompt three values from the user and print the one that is largest.

Example (user input is in blue):
```
First value: -34
Second value: 25
Third value: 16
The largest value is: 25
```

Write a program called sort3.py. Define in this program a function called sort3(x, y, z) that returns the three values x, y, and z in sorted order (a, b, c), where a ≤ b ≤ c. Do not use any built-in Python sorting functions, but you may put if statements inside of other if statements. The program’s main() function should prompt three values from the user and print them sorted.

Example 1 (user input is in blue):

First value: -34
Second value: 16
Third value: 25
Sorted values: (-34, 16, 25)

Example 2:

First value: -34
Second value: 25
Third value: 16
Sorted values: (-34, 16, 25)

Example 3:

First value: 16
Second value: -34
Third value: 25
Sorted values: (-34, 16, 25)

Example 4:

First value: 16
Second value: 25
Third value: -34
Sorted values: (-34, 16, 25)

Example 5:

First value: 25
Second value: -34
Third value: 16
Sorted values: (-34, 16, 25)

Example 6:

First value: 25
Second value: 16
Third value: -34
Sorted values: (-34, 16, 25)

All the previous problems were taken from [JOHNSON] chapters 4 and 6, and from:

Kenneth Lambert.
Fundamentals of Python: From First Programs through Data Structures.
CENGAGE Learning, 2010.
p. 118.

Deliverables

Create a ZIP file called loop_cond.zip containing only the ten programs you wrote (powers.py, table.py, temptable.py, disttable.py, basel.py, pyramid.py, equilateral.py, grade.py, max3.py and sort3.py). Check this two minute Youtube video if you don’t know how to create ZIP files in Windows.

✔ Upload Instructions

To deliver the loop_cond.zip file, please provide the following information:

Request PIN

If this activity was developed by a team of two people, only one person is required to deliver it. No activity will be accepted through e-mail or any other means.

Due date is Friday, February 13, all day up to midnight.

Evaluation

This activity will be evaluated using the following criteria:

-10	One or more programs don’t contain within comments the authors’ personal information.
DA	One or more programs were plagiarized.
10-100	Depending on the amount of problems that were solved correctly.

Problem Solving with Programming