Esta actividad no es para entregar.
Usando gráficas de tortuga, escribe los programas para resolver los problemas que se indican a continuación.
La clase Tree1Fractal dibuja un fractal de árbol como se muestra a continuación:
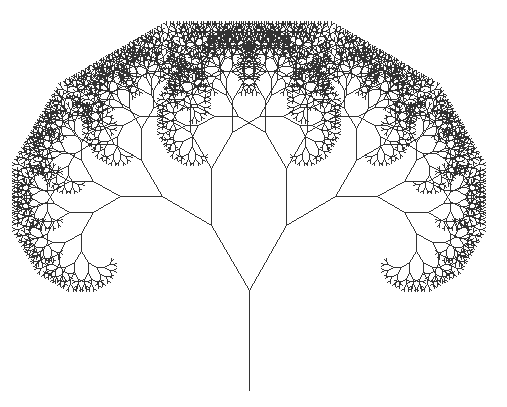
Esta árbol tiene las siguientes características:
La clase Tree2Fractal dibuja un fractal de árbol como se muestra a continuación:
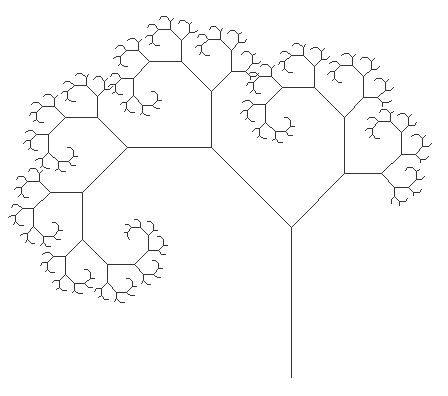
Esta árbol tiene las siguientes características:
La clase PythagoreanTree dibuja un árbol pitagórico como se muestra a continuación:
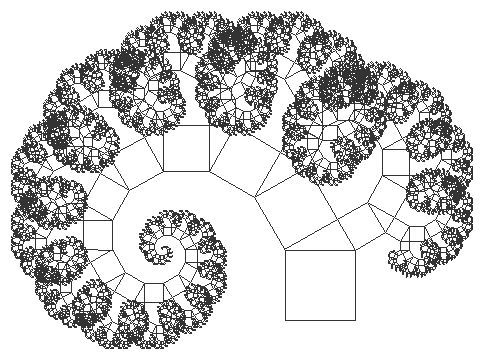
La base de este fractal se muestra en la siguiente figura que ilustra el teorema de Pitágoras:
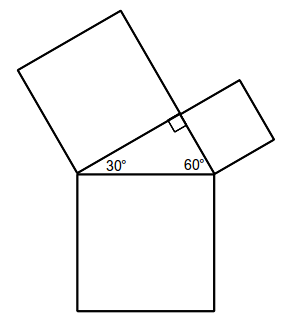
Los cuadros más pequeños del fractal no deben medir menos de 2 píxeles de cada lado.
La clase Koch dibuja un fractal con las curvas de Koch como se muestra a continuación:
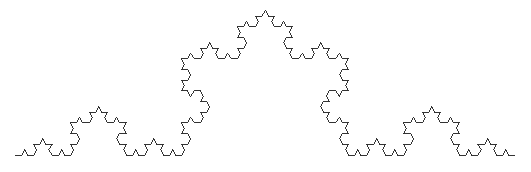
La figura anterior es una curva de Kock de profundidad 4 y longitud 500 píxeles.
El libro de texto explica cómo construir este fractal.
La clase KochSnowFlake dibuja un fractal con las curvas de Koch en forma de copo de nieve como se muestra a continuación:

La figura anterior es un copo de nieve de Kock de profundidad 4 y longitud 300 píxeles.
El libro de texto explica cómo construir este fractal.
La clase Hilbert dibuja un fractal con las curvas de Hilbert como se muestra a continuación:

La figura anterior es una curva de Hilbert de profundida 5, en donde cada trazo es de tamaño 5 píxeles.
El libro de texto explica cómo construir este fractal.
La clase Sierpinsky dibuja un fractal con las curvas de Sierpińsky como se muestra a continuación:

La figura anterior es una curva de Sierpińsky de profundida 5, en donde cada trazo es de tamaño 4 píxeles.
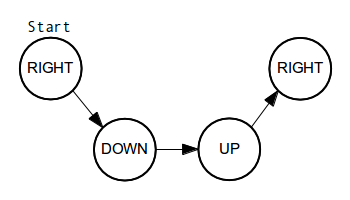
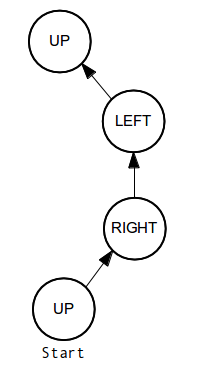
El libro de texto explica cómo construir este fractal. Los siguientes diagramas pueden ayudar a entender mejor el algoritmo:
UP
DOWN
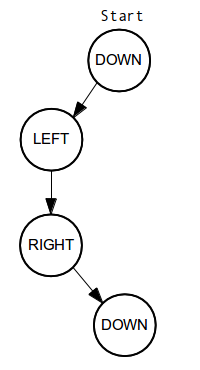
LEFT
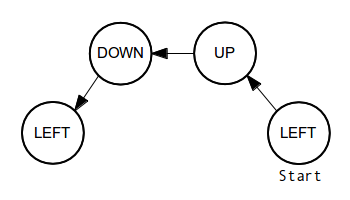
RIGHT